Generation: power-transmission
1 - Introduction
The objective of this tutorial is to understand how the generation works in our modules and how to create a generation in your future bots.
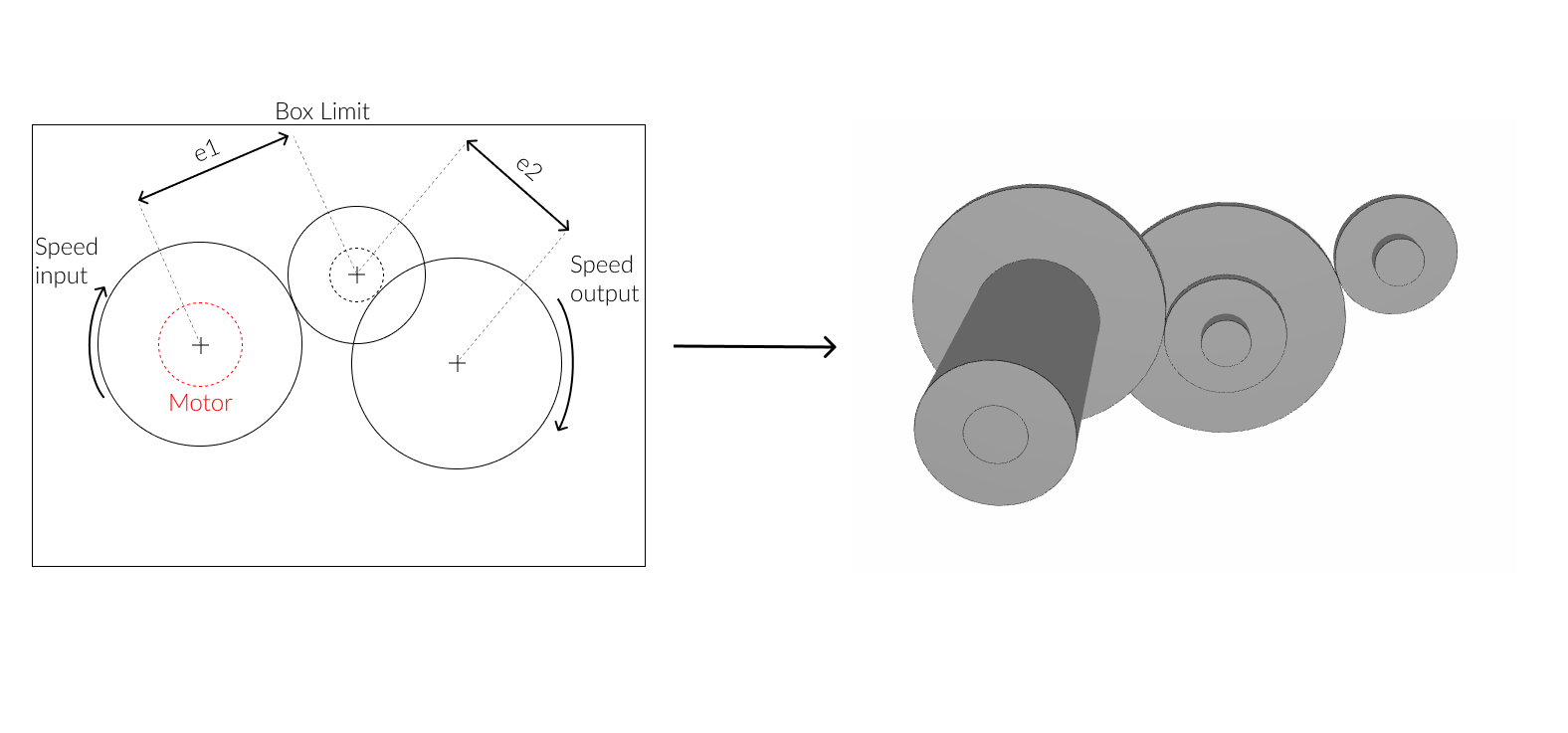
For that, we will use the case of the tutorial 2: construct and optimize a simple reductor constitute by 3 shafts, 4 gears and 1 motor. In this tuto, we will see how to generate all possible solutions before optimizing them by adding the number of teeth. Compare to the bot of the tutorial_2, where the output is composed of some possible solutions, this bot has all possible solutions in output. The number of teeth will allow us to discretize our problem and have the possibility to enumerate all solutions (it's not the case with the tutorial 2 where solutions are based on the diameter).
Like the previous tutorial, we want to optimize the mass of this reductor by fulfilling certain specifications:
-
The ratio between the input and the output speed is imposed
-
The reductor must fit into a box that is imposed
The paramaters that the bot will optimize are the axial distances e1 and e2 and the number of teeth of each gears.
In this tuto we will use the code of the tutorial 2 like a base because we just have to change little things to add a generator. So you have to take back the code you have done in the tutorial 2, if you haven't done this tutorial you can download the file tutorial_2_powertransmission in the github cloud.
2 - Build the bot in 3 steps
For this bot, we will apply the 3 different steps to create a bot, even if one part of the bot is already done with the tuto_2. It will teach you how to apply this strategy if you just want to change some part of a bot.
Before beginning, you have access to tutorial3 in the tutorials folder cloned as explained in the first tutorial.
2.1 - Describe your engineering system
We will take the same description than the previous tuto, 4 classes that represent the principal object of the reductor (Gear, Shaft, Motor and Reductor) and 1 class that represents the connections between them (Mesh). All class definitions will be same except for the Gear where we have to add the number of teeth(z) and the module.
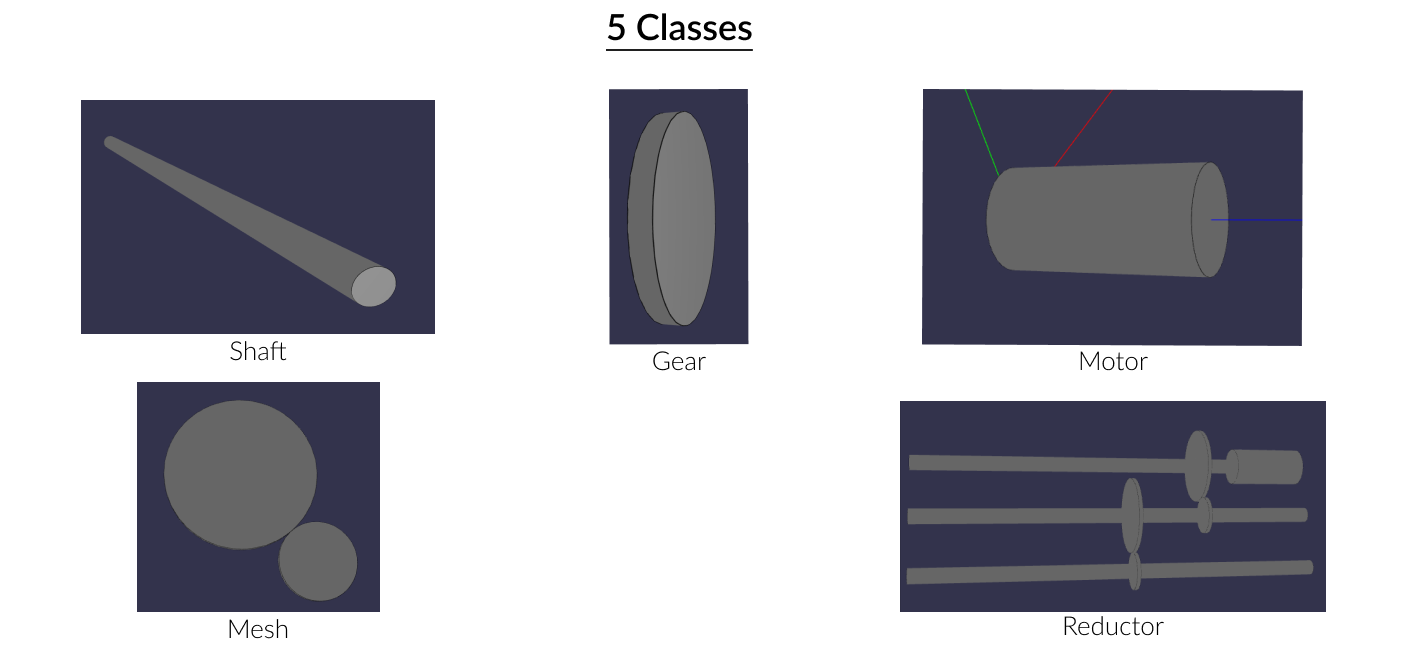
In this tuto, the gears will be now built from their number of teeth, so the necessary parameters to construct them are now the number of teeth, the length and the shaft of the gear. We choose to not put the module into the necessary parameters because we don't need the module if we just want to calculate the ratio. It will be initially set by default to 0.01. The diameter parameter of the gear will be now calculated with the number of teeth and the module.
class Gear(DessiaObject):
def __init__(self, z: int, length: float, shaft: Shaft,module: float = 0.01,name: str=''):
self.z = z
self.length = length
self.shaft=shaft
self.module=module
self.diameter=z*module
DessiaObject.__init__(self,name=name)
self.z_position=02.2 - Define engineering simulations needed
We will keep all the methods developed in the previous tuto particularly :3d methods, calculation of mass and reductor's speed. We just need to add one method on the gear to update the diameter when you change the number of teeth or the module.
def update_diameter(self):
self.diameter=self.z*self.module2.3 - Create elementary generator & optimizer
What is a generator and what is a decision tree?
All necessary classes are coded, we can now see how to build a generator. But firstly, what is a generator?
A generator is an object which can generate all possible solutions of a problem. For that, the generator can use simple for loops, but also decision trees or recursive functions. In this tuto, we will focus on decision trees, because with this method you can do what you want in generation (this is not the case of the other 2 methods which are more limited).
A decision tree is a method that helps you make a decision by separating all possibilities in series of little choices. Like a tree, at each little choice, there are new branches which are formed for all the possible answers. The leaves of the tree which are at the end of the branches represent the final decisions. In a decision tree, the link between the branches are called nodes, and the position of the node in the tree is relative to the origin which is called step.
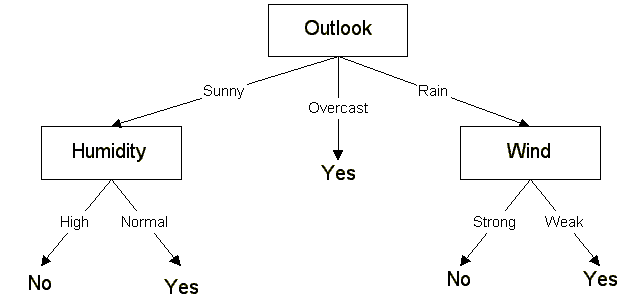
One of the advantages of decision trees is that you can easily cut a branch if the choice made wasn't suitable, and all solutions that depend on this branch will be excluded. That also shows the importance of what choices we put in the first steps of the decision tree. The more these choices are important or divided, the more the decision tree will be efficient because we could exclude more easily a big number of solutions.
To add a decision tree to your code, it's really simple because DessIA has created a special library for that: Dectree. In this library, you can create 2 types of decision tree: Irregular or Regular. The regular is a decision tree where all nodes of a same step created the same number of branches. The irregular is a decision tree where you need to tell for each node the number of branches that will be created (contrary to the regular where you have to tell for each step only). These two types have advantages and drawbacks, that is why we will see both in this tuto. We will begin with the regular and finish with the irregular.
In this tuto, we will generate our solutions by varying the number of teeth of each element. For that, we will use a decision tree where each choice will represent the assignation of a number of teeth at one element. If we take a range of 70 different numbers of teeth, we will have 24010000 solutions (70^4) in the output, it's too many solutions to analyze, that is why we need to add specifications to cut some branches of the decision tree and exclude some solutions. The first specification that we add in the decision tree is the output speed because we can determinate it easily with the number of teeth and that will allow us to exclude the solutions with wrong ratio.
Adding a generator class in your code
To begin, you have to import the dectree librairy in your code :
import dectree as dtAfter that, we have to create a Generator class. For that, we advise you to replace the class InstanciateReductor by the class Generator. Both have same goal (instanciate a reductor), and we also need function that instantiates a reductor in our generator so we will use the same than the class InstanciateReductor. For the initialization of the Generator, we keep the same necessary parameters than the previous class (motor,length_gears and name) and we add the specification of speed_output, the precision and the list z_min_max. The speed output parameter corresponds to the speed that we want in the output. The precision parameter represents how precisely you want to reach the output speed and the z_min_max parameter represents the range of number of teeth that could take our elements.
class Generator(DessiaObject):
def __init__(self,motor: Motor,speed_output: float, precision: float = 0.1,z_min_max: Tuple[int,int]=[4,80],length_gears: float = 0.01, name: str = ''):
self.motor=motor
self.speed_output=speed_output
self.length_gears=length_gears
self.z_min_max=z_min_max
self.precision=precision
self.speed_input=motor.speed
DessiaObject.__init__(self,name=name)
def instanciate(self):
shafts = [Shaft(pos_x=0, pos_y=0, length=0.1), Shaft(pos_x=0, pos_y=0, length=0.1),
Shaft(pos_x=0, pos_y=0, length=0.1)]
gear1 = Gear(z=1, length=self.length_gears, shaft=shafts[0])
gear2 = Gear(z=1, length=self.length_gears, shaft=shafts[1])
gear3 = Gear(z=1, length=self.length_gears, shaft=shafts[1])
gear4 = Gear(z=1, length=self.length_gears, shaft=shafts[2])
meshes=[Mesh(gear1, gear2),Mesh(gear3, gear4)]
reductor = Reductor(self.motor, shafts, meshes)
return reductorCreate a function with a decision tree
The next step is to create a function generate() that will allow us to build the decision tree and return all possible solutions. The command to create a regular decision tree is: dt.RegularDecisionTree(list_node). The list_node parameter that we need to create the regular decision tree is a list corresponding to the number of choices that we have at each step in the decision tree (in a regular decision tree, all nodes at a same step have the same available choices). In our case, we have at each step the choice between all the possible numbers of teeth defined by the range z_min_max. We have 4 gears, the list_node parameter is therefore equal to [z_min_max[1]-z_min_max[0]] x 4.
Before creating the decision tree, we have to instantiate a reductor with the instantiate function. In this tuto, we choose to change the number of teeth directly in the reductor when we browse the decision tree. You can also save the different parameter and construct the reductor at the end of the decision tree but it's generally easier to instantiate it at the beginning.
def generate(self):
list_node=[]
reductor=self.instanciate()
for meshe in reductor.meshes:
for gear in [meshe.gear1,meshe.gear2]:
list_node.append(self.z_min_max[1]-self.z_min_max[0])
tree=dt.RegularDecisionTree(list_node)We also need a reference to know which gear corresponds to which step. For that, we will create a list of gears, where its indices will correspond to the steps.
def generate(self):
list_node=[]
list_gear=[]
reductor=self.instanciate()
for meshe in reductor.meshes:
for gear in [meshe.gear1,meshe.gear2]:
list_node.append(self.z_min_max[1]-self.z_min_max[0])
list_gear.append(gear)
tree=dt.RegularDecisionTree(list_node)
Then, we can start browsing the decision tree by creating a while loop with the condition ' not tree.finished '. The parameter finished of the tree will be True when the tree is totally browsed.
After that, we have to put at the end of the while loop the function tree.NextNode(valid), that will allow to pass to the next node for the next iteration of the while loop. The parameter valid is a boolean that shows the suitability of a choice at a node. If not, the tree automatically cuts the next branches of this node. We have to initiate this parameter at True at each iteration of the while loop and if a condition said that the node is not suitable, we put the valid parameter at false.
To save the solutions of reductor we found in the decision tree, we also have to create a list_reductor before the while loop. This is the list returned at the end of the function generate:
def generate(self):
list_node=[]
list_gear=[]
reductor=self.instanciate()
for meshe in reductor.meshes:
for gear in [meshe.gear1,meshe.gear2]:
list_node.append(self.z_min_max[1]-self.z_min_max[0])
list_gear.append(gear)
tree=dt.RegularDecisionTree(list_node)
list_reductor=[]
while not tree.finished:
valid=True
tree.NextNode(valid)
return list_reductor
Update an object in a decision tree
Like explained, we have to update the number of teeth elements at each choice of the decision tree. For that, we need the browsed node and we can access it with the parameter current_node of the tree. This function returns a list made of the current node but also those browsed before to access this node. To only have the position of the node browsed we have to take the last element of this list. To update, we must be careful because the position of the node will not be exactly equal to the number of teeth, we have to add the minimum border of the z_min_max range (the positions of the nodes always begins at 0). To assign the number of teeth on the right gear, we can use the list_gear and the length of the node corresponding at the current step. We just have to subtract 1 to the length because the positions of lists begin at 0.
def generate(self):
list_node=[]
list_gear=[]
reductor=self.instanciate()
for meshe in reductor.meshes:
for gear in [meshe.gear1,meshe.gear2]:
list_node.append(self.z_min_max[1]-self.z_min_max[0])
list_gear.append(gear)
tree=dt.RegularDecisionTree(list_node)
list_reductor=[]
while not tree.finished:
valid=True
node = tree.current_node
list_gear[len(node)-1].z=node[-1]+self.z_min_max[0]
tree.NextNode(valid)
return list_reductor
Adding a condition in a decision tree
Now, we can add our first condition in our generation and we will begin by the speed specification. The speed condition can be verified when all the numbers of teeth are chosen, so it's a condition for the final step of the tree. To apply a condition at a particular step, we have to put an if condition in the while loop which begins by ' if len(node) '. In our case, it's the final step, so the condition is ' if len(node)==len(list_gear):' (the length of the list gear corresponds to the number total of steps).
After that, we just have to put the condition for the verification of speed. Remember that we have the precision parameter that represents how precisely you want to reach the output speed, so we will have a minimal and a maximal border for this condition (self.speed_output*(1-self.precision) and self.speed_output*(1+self.precision)). The speed output can be calculated by the function speed_output of the reductor. If the speed condition is valid, we can put a deep copy of the reductor in the list list_reductor, if not, we put the parameter valid at False. The deep copy is necessary for saving the current reductor because we will change the number of teeth in the next iterations.
def generate(self):
list_node=[]
list_gear=[]
reductor=self.instanciate()
for meshe in reductor.meshes:
for gear in [meshe.gear1,meshe.gear2]:
list_node.append(self.z_min_max[1]-self.z_min_max[0])
list_gear.append(gear)
tree=dt.RegularDecisionTree(list_node)
list_reductor=[]
while not tree.finished:
valid=True
node = tree.current_node
list_gear[len(node)-1].z=node[-1]+self.z_min_max[0]
if len(node)==len(list_gear):
if reductor.speed_output() > self.speed_output*(1-self.precision) and reductor.speed_output() < self.speed_output*(1+self.precision):
list_reductor.append(copy.deepcopy(reductor))
else:
valid = False
tree.NextNode(valid)
return list_reductor
Changes on an optimizer with a generator
For the moment, we will test the generator with just this condition, but before launching the script, we have to modify some little things in the optimizer:
- In the objective function, we can delete the line where the speed conditions are tested because we already verify them in the generator. In the init, we can also remove the parameter speed_output.
def objective(self, x):
self.reductor.update(x)
speed = self.reductor.speed_output()
functional = 0
previous_radius_gear_1 = 0
previous_radius_gear_2 = 0
previus_radius_shaft = 0
- In the optimize function, we don't need to return a list of optimized solutions for the workflow part because the generator will already generate a list of solutions, we just have to optimize all of them to obtain a list of optimized solutions.
def optimize(self, max_loops: int =1000):
valid = True
count = 0
while valid and count < max_loops:
x0 = self.cond_init()
self.reductor.update(x0)
res = minimize(self.objective, x0, bounds=self.bounds)
count += 1
if res.fun < 10 and res.success:
print(count)
self.reductor.update(res.x)
return self.reductor
return self.reductor- We also have to change the x vector by removing the diameter of the gears (because we have already chosen the number of teeth in the generator and the module will be calculated with the position of shafts). So the calculation of border and the update function of the reductor need to be changed. Now, in the update function, the diameter of the gears will be calculated by using the center_distance and the ratio of teeth number.
def __init__(self, reductor: Reductor, x_min_max: Tuple[float, float], y_min_max: Tuple[float, float], name: str =''):
self.reductor = reductor
self.x_min_max = x_min_max
self.y_min_max= y_min_max
DessiaObject.__init__(self,name=name)
bounds = []
for shaft in reductor.shafts:
bounds.append([x_min_max[0], x_min_max[1]])
bounds.append([y_min_max[0], y_min_max[1]])
self.bounds = boundsdef update(self, x):
i=0
for shaft in self.shafts:
shaft.pos_x=x[i]
shaft.pos_y=x[i+1]
i+=2
for mesh in self.meshes:
shaft_gear1=mesh.gear1.shaft
shaft_gear2=mesh.gear2.shaft
center_distance = ((shaft_gear1.pos_x-shaft_gear2.pos_x)**2+(shaft_gear1.pos_y-shaft_gear2.pos_y)**2)**(1/2)
mesh.gear1.diameter = 2*center_distance*mesh.gear1.z/(mesh.gear1.z+mesh.gear2.z)
mesh.gear2.diameter = 2*center_distance*mesh.gear2.z/(mesh.gear1.z+mesh.gear2.z)
mesh.gear1.module= mesh.gear1.diameter /mesh.gear1.z
mesh.gear2.module= mesh.gear1.module
self.mass_reductor=self.mass() Script test for a generator
For the script that we will launch, you can create a new or modify the script of tutorial 2. To launch the generator, we need to create a motor and to specify the speed output condition and the range of teeth number. We advice you to put a small range, otherwise, the calculation will be very long (we choose in our script [4,30]). After that, we have to create an optimizer and launch the optimize function for each reductor generated with a for loop. Remember that we also have to put the condition of box limit in the optimizer.
import tutorials.tutorial3_powertransmission_generator as objects
motor = objects.Motor(diameter=0.1, length=0.2, speed=120)
generator=objects.Generator(motor=motor,speed_output=600,z_min_max=[4,30])
list_reductor=generator.generate()
for reductor in list_reductor:
optimizer = objects.Optimizer(reductor=reductor, x_min_max=[-1,1], y_min_max=[-1,1])
optimizer.optimize()
If you run this script, you will observe that we need to wait a long time before it ends (You can stop the code if you want when the first 10 solutions are optimized. To stop the code, you have to press CTRL+C in the console). It's normal because our condition in the generator is on the final step, so we can just cut the last branches of the tree. But if you verify in the console the length of the list_reductor, you will see that we have a big number of solutions (11504 in the case of our script), many more than that we have with just the optimizer. If you plot the 3D (with babylonjs()) of the different optimized solutions, you will see that the solutions are very similar between them. It's normal because the solutions are found by browsing a decision tree so we have in the list_reductor all the solutions that have branches in common grouped together.
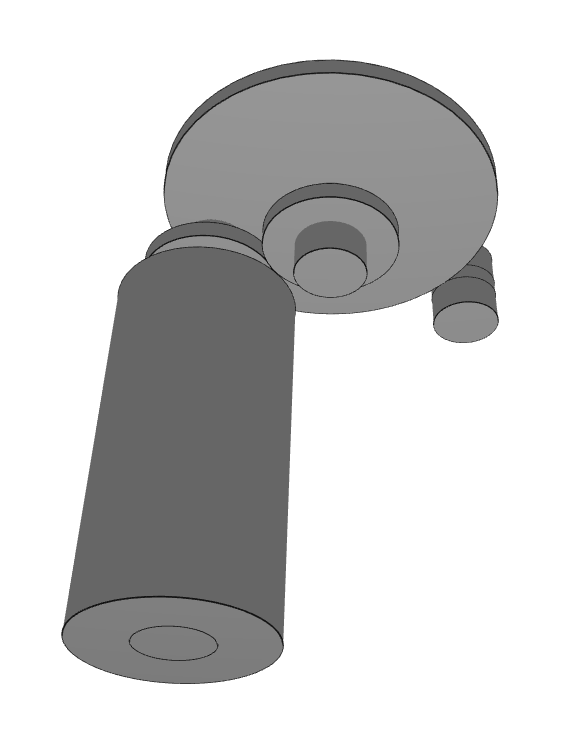
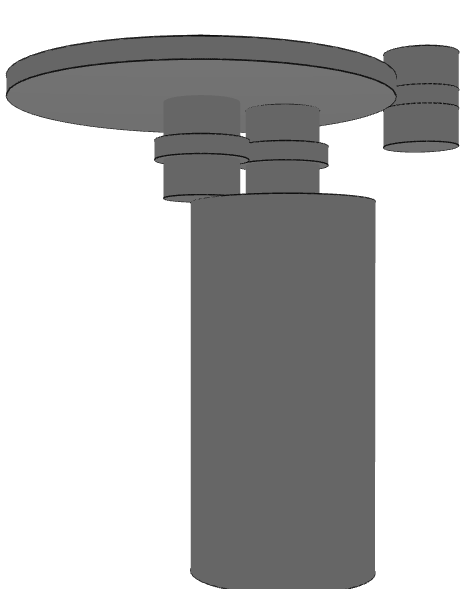
Two other examples of adding a condition
Now, we will see to add 2 other conditions in the generator. The first concerns the verification of GCD between the gears that meshed together (for acoustical problems) and the second is a condition on the ratio of meshes which must follow the same type of ratio than the speed (ratio>1 or ratio<1).
Firstly, we have to use GCD function of math module to calculate the gcd on the number of teeth of gears that are meshed together and check if it's equal to 1. If the condition is not valid, we set the valid parameter on False. To apply this rule at the right moment, we have to put a condition on the node length, the step where the number of teeth of the first two gears are chosen is the step 2 and it's the step 4 for the last two gears. At these steps, we know that the gears we want to test are the gear of the current step (len(node)-1) and the gear of the previous step (len(node)-2). Now, we have all that we need to add this condition.
def generate(self):
list_node = []
list_gear = []
reductor = self.instanciate()
for meshe in reductor.meshes:
for gear in [meshe.gear1, meshe.gear2]:
list_node.append(self.z_min_max[1]-self.z_min_max[0])
list_gear.append(gear)
tree=dt.RegularDecisionTree(list_node)
list_reductor = []
while not tree.finished:
valid = True
node = tree.current_node
list_gear[len(node)-1].z = node[-1]+self.z_min_max[0]
if len(node) == 2 or len(node) == 4:
if math.gcd(list_gear[len(node)-1].z,list_gear[len(node)-2].z) != 1:
valid = False
if len(node)==len(list_gear) and valid:
if reductor.speed_output() > self.speed_output*(1-self.precision) and reductor.speed_output() < self.speed_output*(1+self.precision):
list_reductor.append(copy.deepcopy(reductor))
else:
valid = False
tree.NextNode(valid)
return list_reductorSecondly, we just have to verify if the number of teeth of the previous gear is inferior or superior (depends on the ratio of the speed) than the number of teeth of the current gear. If the input speed is higher than the output speed, the number of teeth of the previous gear also needs to be higher than the number of teeth of the current gear, and it's the contrary if the input speed is smaller than output speed. For the steps of the tree where this rule is applied, there is the same GCD rule (step 2 and 4). This rule is very useful because it deletes all solutions which are not interesting because the gear diameters are not optimal to reach the output speed.
def generate(self):
list_node = []
list_gear = []
reductor = self.instanciate()
for meshe in reductor.meshes:
for gear in [meshe.gear1, meshe.gear2]:
list_node.append(self.z_min_max[1]-self.z_min_max[0])
list_gear.append(gear)
tree=dt.RegularDecisionTree(list_node)
list_reductor = []
while not tree.finished:
valid = True
node = tree.current_node
list_gear[len(node)-1].z = node[-1]+self.z_min_max[0]
if len(node) == 2 or len(node) == 4:
if math.gcd(list_gear[len(node)-1].z,list_gear[len(node)-2].z) != 1:
valid = False
if self.speed_input < self.speed_output:
if node[-2] <= node[-1]:
valid = False
else:
if node[-2] >= node[-1]:
valid = False
if len(node)==len(list_gear) and valid:
if reductor.speed_output() > self.speed_output*(1-self.precision) and reductor.speed_output() < self.speed_output*(1+self.precision):
list_reductor.append(copy.deepcopy(reductor))
else:
valid = False
tree.NextNode(valid)
return list_reductorYou can add a condition in the if concerning the speed verification to not do the test if the parameter valid is false (the last step is also the step 4 so we need to verify if the precedent condition are valid before saving a solution).
After adding these two conditions, you can restart the script and see that the number of solutions has decreased (3690 in our case, almost divided by 4). With these two other conditions, the optimization time will be smaller and we have targeted the most interesting solutions.
With this two other examples, you now have keys to create your generation and add conditions in it.